Binary Tree Data Structure
click here to read this in medium
Binary Tree Traversals and problem solving

💡 Common terms :-
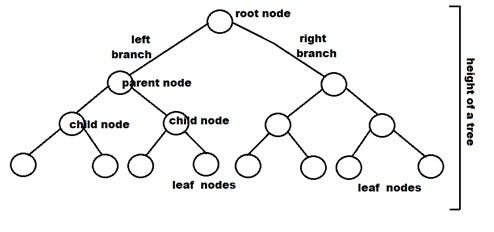
In this article we will be Discussing different tree traversals and problem solving based on these tree traversals.
Note: All the code is in JAVA.

🌴 Tree Traversals : (Depth First Traversals)
- In-Order
- Pre-Order
- Post-Order
The goal of these traversals is to visit all the nodes in the binary tree.
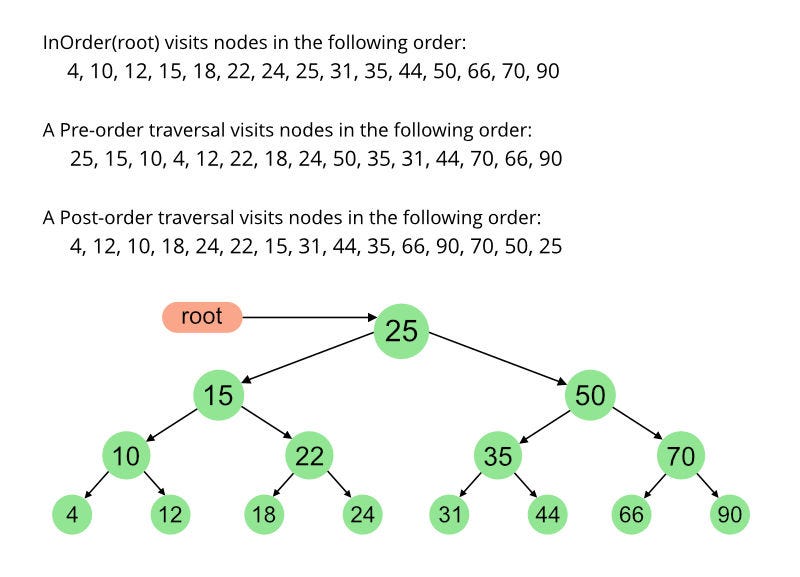
In-Order Traversal :-
In this In-order →
1. First visit all nodes on the left
2. visit present node
3. Then visit all nodes on the right
void inorder(TreeNode root) {
if(root==null){
return;
}
inorder(root.left);
System.out.println(root.val);
inorder(root.right);
}
LeetCode submission → https://leetcode.com/problems/binary-tree-inorder-traversal/submissions/679456795/
Pre-Order Traversal:-
Here we follow →
1. First visit present node
2. visit all nodes on the left
3. Then visit all nodes on the right
void preorder(TreeNode r){
if(r==null){
return;
}
System.out.println(r.val);
preorder(r.left);
preorder(r.right);
}
LeetCode submission → https://leetcode.com/problems/binary-tree-preorder-traversal/submissions/908748627/
Post-Order Traversal:-
Here we follow →
1. First visit all nodes on the left
2. Then visit all nodes on the right
3. Visit present node
void postOrder(TreeNode r) {
if(r ==null) {
return;
}
postOrder(r.left);
postOrder(r.right);
System.out.println(r.val);
}
LeetCode submission → https://leetcode.com/problems/binary-tree-postorder-traversal/submissions/908750442/
🛠 Level Order Traversal : (Breadth First Traversal)
Here the goal is to print the tree nodes level by level. My Implementation
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
solve(root,0);
return res;
}
public void solve(TreeNode n,int level){
if(n==null)return ;
if(res.size()>level){
res.get(level).add(n.val);
}else{
List<Integer> t = new ArrayList<>();
t.add(n.val);
res.add(t);
}
solve(n.left,level+1);
solve(n.right,level+1);
}
}
LeetCode submission → https://leetcode.com/problems/binary-tree-level-order-traversal/submissions/677053619/
But BFS says to maintain the queue where we first add root node and loop by pop the node and add the children to the queue.Which also gives the similar result with same runtime.
🥷 Example problem 1
Sum Root to Leaf Numbers - LeetCode
Here we need to find a way to get all possible numbers formed by traversing from the root node to each leaf node. Then sum it up. So after observing the problem statement, we can get an idea that we need to use preorder Traversal. But the Question is How we can identify the different paths from root to leaf node? So I got the idea to add an edge case to the preorder traversal saying hey if the present node leaf node here the code for it.
class Solution {
int sum = 0;
public int sumNumbers(TreeNode root) {
preorder(root,new StringBuilder());
return sum;
}
public void preorder(TreeNode node, StringBuilder sb){
if (node == null) return;
sb.append(node.val);
if (node.left == null && node.right == null) {
sum += Integer.parseInt(sb.toString());
}
preorder(node.left, sb);
preorder(node.right, sb);
sb.deleteCharAt(sb.length() - 1);
}
}
// https://leetcode.com/problems/sum-root-to-leaf-numbers/submissions/908758869/
🚀 Example problem 2
Binary Tree Maximum Path Sum - LeetCode
This is also a very interesting problem. Where we need to find the Path where we can get the maximum Sum by adding the node values. In these case where we need to see all the nodes from the bottom of the tree. We have to go with postOrder kind of approach to solve this problem. Here is my solution.
class Solution {
int final_max = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
solve(root);
return final_max;
}
public int solve(TreeNode root){
if(root==null){return 0;}
int leftMax = solve(root.left);
int rightMax = solve(root.right);
int send_top = Math.max(Math.max(leftMax,rightMax)+root.val,root.val);
int comMax = Math.max(leftMax+rightMax+root.val,send_top);
final_max = Math.max(final_max,comMax);
return send_top;
}
}
// https://leetcode.com/problems/binary-tree-maximum-path-sum/submissions/909178204/
Thank you…!